Trong lĩnh vực toán học, việc tìm hiểu về đường tròn ngoại tiếp tam giác không chỉ là một bài toán hình học thuần túy mà còn có nhiều ứng dụng thực tiễn trong kiến trúc, xây dựng và thiết kế. Bài viết này sẽ giúp bạn hiểu rõ về cách tính bán kính đường tròn ngoại tiếp tam giác cùng các ứng dụng của nó trong thực tế.
Khái Niệm Cơ Bản về Đường Tròn Ngoại Tiếp Tam Giác
Định Nghĩa
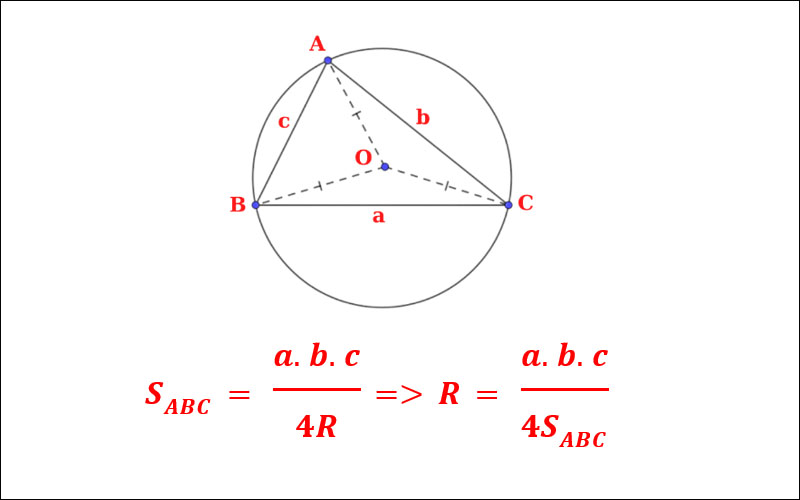
Đường tròn ngoại tiếp tam giác là đường tròn đi qua cả ba đỉnh của tam giác. Tâm của đường tròn ngoại tiếp chính là giao điểm của ba đường trung trực của tam giác. Bán kính của đường tròn này được gọi là bán kính đường tròn ngoại tiếp tam giác.

Đặc Điểm Quan Trọng
- Tâm đường tròn ngoại tiếp cách đều ba đỉnh của tam giác
- Tâm đường tròn ngoại tiếp có thể nằm trong, trên hoặc ngoài tam giác tùy thuộc vào loại tam giác
- Với mỗi tam giác, chỉ tồn tại duy nhất một đường tròn ngoại tiếp
Các Phương Pháp Tính Bán Kính Đường Tròn Ngoại Tiếp
Phương Pháp 1: Sử Dụng Công Thức Cơ Bản
Bán kính đường tròn ngoại tiếp (R) được tính theo công thức:
R = abc/(4S)Trong đó:
- a, b, c là độ dài ba cạnh của tam giác
- S là diện tích tam giác
Phương Pháp 2: Sử Dụng Công Thức Mở Rộng
Bán kính có thể được tính thông qua:
R = abc/[4√(p(p-a)(p-b)(p-c))]Với p là nửa chu vi tam giác:
p = (a + b + c)/2
Phương Pháp 3: Sử Dụng Hàm Lượng Giác
Với tam giác có góc A, B, C:
R = a/(2sinA) = b/(2sinB) = c/(2sinC)Ứng Dụng Thực Tiễn
Trong Xây Dựng và Kiến Trúc
- Thiết kế mái vòm và cấu trúc cong
- Tính toán khoảng cách và độ cong của các công trình
- Quy hoạch không gian và bố trí các công trình công cộng
Xem thêm Công Thức Tính Diện Tích Xung Quanh: Hướng Dẫn Chi Tiết và Ứng Dụng
Trong Thiết Kế Công Nghiệp
- Thiết kế các bộ phận máy móc có hình dạng cong
- Tối ưu hóa không gian trong thiết kế sản phẩm
- Tính toán độ cong cho các vật liệu composite
Trong Nghệ Thuật và Thiết Kế
- Tạo các mẫu hình học trong nghệ thuật
- Thiết kế logo và đồ họa
- Trang trí nội thất và ngoại thất

Ví Dụ Minh Họa
Bài Toán 1
Cho tam giác ABC có các cạnh:
- a = 13 cm
- b = 14 cm
- c = 15 cm
Tính bán kính đường tròn ngoại tiếp.
Lời giải:
- Tính nửa chu vi p:
p = (13 + 14 + 15)/2 = 21 cm - Tính diện tích S theo công thức Heron:
S = √[21(21-13)(21-14)(21-15)] S = √(21 × 8 × 7 × 6) S = √7056 = 84 cm² - Tính bán kính R:
R = (13 × 14 × 15)/(4 × 84) = 8,125 cm
Bài Toán 2
Cho tam giác vuông ABC có:
- Cạnh góc vuông a = 6 cm
- Cạnh góc vuông b = 8 cm
Tính bán kính đường tròn ngoại tiếp.
Lời giải:
- Tính cạnh huyền c theo định lý Pytago: Copy
c = √(6² + 8²) = 10 cm - Với tam giác vuông, bán kính đường tròn ngoại tiếp: Copy
R = c/2 = 5 cm
Những Lưu Ý Quan Trọng
Khi Nào Cần Sử Dụng
- Cần tính toán chính xác các kích thước trong thiết kế
- Muốn tối ưu hóa không gian và vật liệu
- Cần đảm bảo tính thẩm mỹ trong thiết kế
Những Sai Lầm Cần Tránh
- Nhầm lẫn giữa bán kính đường tròn ngoại tiếp và nội tiếp
- Quên kiểm tra điều kiện tồn tại của tam giác
- Sử dụng sai đơn vị đo
- Bỏ qua việc kiểm tra kết quả
Xem thêm Phân tích toàn diện về nguyên hàm của cos bình x và ứng dụng trong thực tiễn
Tổng Kết
Việc nắm vững cách tính bán kính đường tròn ngoại tiếp tam giác không chỉ giúp giải quyết các bài toán hình học mà còn có nhiều ứng dụng thực tiễn quan trọng. Thông qua các phương pháp và ví dụ trên, chúng ta đã thấy được tầm quan trọng của kiến thức này trong nhiều lĩnh vực khác nhau.
Thông Tin Liên Hệ
Để được tư vấn thêm về các ứng dụng của toán học trong công tác xã hội và phát triển cộng đồng, vui lòng liên hệ:
- Hotline: 0909 333 666
- Email: [email protected]
- Website: sdrc.com.vn
Trung tâm Nghiên cứu – Tư vấn Công tác Xã hội & Phát triển Cộng đồng (SDRC) luôn sẵn sàng hỗ trợ bạn trong việc áp dụng các kiến thức toán học vào thực tiễn, góp phần phát triển cộng đồng một cách hiệu quả và bền vững.