Nhận Biết Và Phân Biệt Hình Đa Diện Trong Hình Học Không Gian

Hình học không gian là một phần quan trọng trong chương trình toán học phổ thông, trong đó việc nhận biết và phân biệt các loại hình đa diện đóng vai trò then chốt. Bài viết này sẽ giúp các bạn học sinh hiểu rõ về hình đa diện và lý giải câu hỏi hình nào sau đây không phải là hình đa diện.

Định Nghĩa Và Đặc Điểm Của Hình Đa Diện

Khái Niệm Cơ Bản

Hình đa diện là hình được tạo thành từ một số hữu hạn mặt phẳng (đa giác), trong đó:

• Mỗi cạnh của một mặt là cạnh chung của đúng hai mặt
• Hai mặt bất kỳ không đồng phẳng hoặc không giao nhau
• Hình phải kín và có thể tích

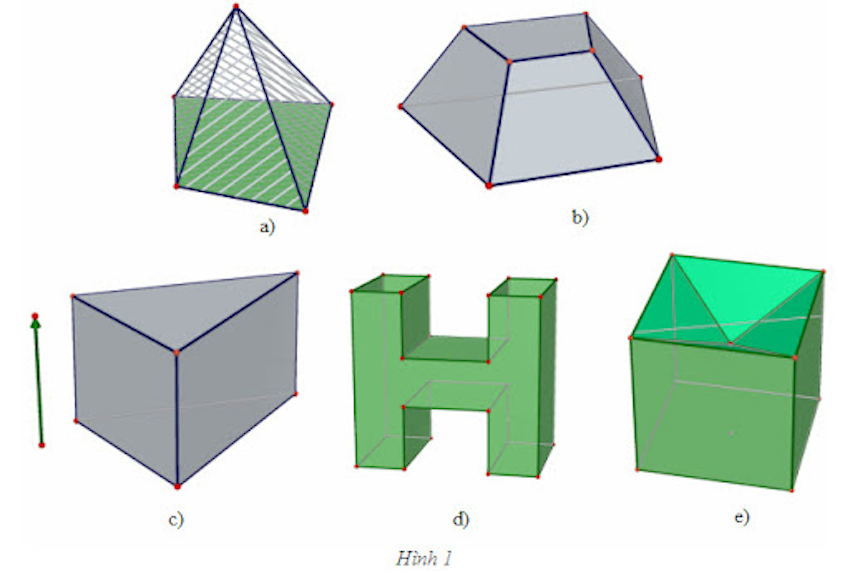
Các Yếu Tố Cơ Bản

1. Mặt: Là các đa giác giới hạn hình đa diện
2. Cạnh: Là các đoạn thẳng nơi hai mặt giao nhau
3. Đỉnh: Là điểm nơi ba cạnh trở lên gặp nhau
4. Góc đa diện: Được tạo bởi ba mặt trở lên

Những Hình Không Phải Là Hình Đa Diện

Hình Tròn Xoay

1. Hình trụ tròn xoay
   • Có hai đáy là hình tròn
   • Mặt xung quanh cong
   • Không có mặt phẳng bao quanh
2. Hình nón tròn xoay
   • Đáy là hình tròn
   • Mặt bên cong
   • Có một đỉnh
3. Hình cầu
   • Không có mặt phẳng
   • Bề mặt cong đều
   • Không có đỉnh và cạnh

Xem thêm Hướng Dẫn Chi Tiết Giải Bài Tập Về Hình Vuông ABCD Cạnh a

Hình Hỗn Hợp

1. Hình bán cầu
   • Một nửa hình cầu
   • Có một mặt phẳng và một mặt cong
2. Hình trụ cụt
   • Hình trụ bị cắt bởi mặt phẳng xiên
   • Có một đáy tròn và một đáy elip
3. Hình nón cụt
   • Hình nón bị cắt bởi mặt phẳng song song với đáy
   • Có hai đáy tròn không bằng nhau

Cách Nhận Biết Hình Đa Diện

Đặc Điểm Nhận Dạng

1. Tiêu chí về mặt:
   • Tất cả các mặt phải là đa giác
   • Số mặt phải hữu hạn
   • Các mặt phải liên tiếp nhau
2. Tiêu chí về cạnh:
   • Cạnh phải là đoạn thẳng
   • Mỗi cạnh thuộc về đúng hai mặt
   • Các cạnh tạo thành khung kín
3. Tiêu chí về đỉnh:
   • Đỉnh là điểm giao của các cạnh
   • Mỗi đỉnh phải thuộc ít nhất ba cạnh

Ví Dụ Minh Họa

1. Hình đa diện đúng:
   • Hình lập phương
   • Hình chóp đều
   • Hình lăng trụ đều
   • Hình tứ diện đều
2. Không phải hình đa diện:
   • Hình trụ (có mặt cong)
   • Hình nón (có mặt cong)
   • Hình cầu (toàn mặt cong)

Phương Pháp Kiểm Tra

Các Bước Kiểm Tra

1. Xem xét bề mặt:
   • Kiểm tra tính phẳng của các mặt
   • Đếm số mặt
   • Xác định hình dạng các mặt
2. Kiểm tra cạnh và đỉnh:
   • Đếm số cạnh và đỉnh
   • Xác định mối quan hệ giữa các cạnh
   • Kiểm tra tính liên tục
3. Kiểm tra tính khép kín:
   • Đảm bảo không có khoảng hở
   • Xác nhận tính liên tục của bề mặt

Xem thêm Hướng Dẫn Chi Tiết Giải Bài Tập Lũy Thừa Lớp 6

Lưu Ý Quan Trọng

1. Những sai lầm thường gặp:
   • Nhầm lẫn với hình có mặt cong
   • Bỏ sót các yếu tố cần kiểm tra
   • Không kiểm tra tính khép kín
2. Kỹ năng cần thiết:
   • Quan sát tỉ mỉ
   • Phân tích logic
   • Áp dụng định nghĩa chính xác

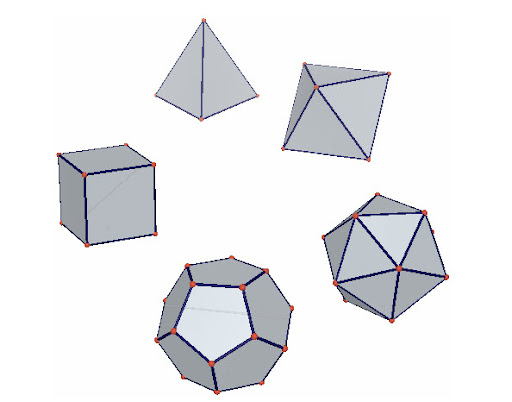
Ứng Dụng Trong Thực Tế

Trong Kiến Trúc

1. Thiết kế nhà ở:
   • Hình hộp chữ nhật
   • Mái nhà hình chóp
   • Các khối đa diện phức hợp
2. Công trình công cộng:
   • Các tòa nhà cao tầng
   • Cấu trúc mái vòm
   • Thiết kế cầu thang

Trong Đời Sống

1. Đồ vật hàng ngày:
   • Hộp đựng đồ
   • Bao bì sản phẩm
   • Đồ chơi xếp hình
2. Trong nghệ thuật:
   • Điêu khắc
   • Trang trí nội thất
   • Thiết kế sản phẩm

Bài Tập Và Hướng Dẫn Giải

Bài Tập Mẫu

1. Xác định hình nào sau đây không phải là hình đa diện: a) Hình hộp chữ nhật b) Hình trụ tròn xoay c) Hình chóp tam giác đều d) Hình nón

Lời giải:

- Hình b) và d) không phải là hình đa diện vì:
  + Hình trụ có mặt xung quanh cong
  + Hình nón có mặt bên cong
- Các hình còn lại là hình đa diện vì được giới hạn bởi các mặt phẳng

Phương Pháp Giải

1. Phân tích đặc điểm:
   • Xác định các mặt
   • Kiểm tra tính phẳng
   • Đếm số cạnh và đỉnh
2. So sánh với định nghĩa:
   • Đối chiếu với tiêu chí
   • Loại trừ các trường hợp không phù hợp

Dịch Vụ Hỗ Trợ Từ SDRC

Chương Trình Học Tập

Trung tâm Nghiên cứu – Tư vấn Công tác Xã hội & Phát triển Cộng đồng (SDRC) cung cấp:

1. Khóa học hình học không gian:
   • Lý thuyết cơ bản
   • Bài tập mẫu
   • Phương pháp giải
2. Tài liệu học tập:
   • Sách bài tập
   • Video bài giảng
   • Đề thi mẫu

Xem thêm Hướng Dẫn Chi Tiết: Giải Phương Trình 1 + sinx + cosx + tanx = 0

Hỗ Trợ Học Sinh

1. Tư vấn học tập:
   • Giải đáp thắc mắc
   • Hướng dẫn phương pháp học
   • Luyện thi các cấp
2. Dịch vụ kèm học:
   • Học nhóm
   • Học 1-1
   • Ôn thi chuyên đề

Thông Tin Liên Hệ

Để được tư vấn và hỗ trợ học tập, vui lòng liên hệ:

• Hotline: 0909 333 666
• Email: [email protected]
• Website: sdrc.com.vn

SDRC luôn sẵn sàng đồng hành cùng các em trong hành trình học tập. Hãy liên hệ với chúng tôi để được hỗ trợ tốt nhất!