Trong toán học, việc tính diện tích xung quanh của các hình học cơ bản là một khái niệm quan trọng và được áp dụng rộng rãi trong nhiều lĩnh vực, từ kiến trúc, xây dựng đến các ngành khoa học kỹ thuật. Bài viết này sẽ cung cấp cho bạn một cái nhìn tổng quan về các công thức tính diện tích xung quanh của các hình học phổ biến và cách áp dụng chúng trong thực tế. Ngoài ra, chúng ta cũng sẽ nhắc đến trang web sdrc.com.vn như một nguồn tài liệu hữu ích cho việc học tập và tra cứu.
1. Diện Tích Xung Quanh Hình Hộp Chữ Nhật
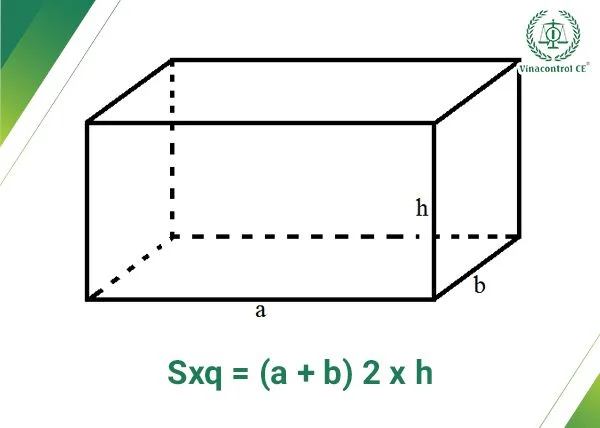
Hình hộp chữ nhật là một trong những hình học cơ bản và phổ biến nhất. Để tính diện tích xung quanh của hình hộp chữ nhật, chúng ta sử dụng công thức:
$$S_{xq} = 2h(a + b)$$
Trong đó:
- (S_{xq}) là diện tích xung quanh
- (h) là chiều cao của hình hộp chữ nhật
- (a) là chiều dài
- (b) là chiều rộng
Ví dụ, nếu bạn có một hình hộp chữ nhật với chiều dài 5m, chiều rộng 3m và chiều cao 4m, diện tích xung quanh sẽ là:
$$S_{xq} = 2 \times 4 \times (5 + 3) = 64 \, m^2$$
2. Diện Tích Xung Quanh Hình Trụ
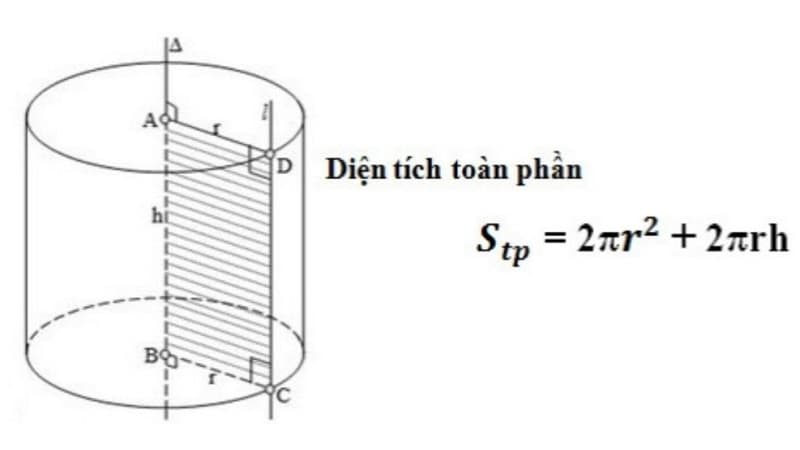
Hình trụ là một hình dạng phổ biến trong kiến trúc và xây dựng. Công thức tính diện tích xung quanh của hình trụ là:
$$S_{xq} = 2\pi rh$$
Trong đó:
- (r) là bán kính đáy của hình trụ
- (h) là chiều cao của hình trụ
- (\pi) là hằng số Pi (xấp xỉ 3.14)
Ví dụ, nếu bạn có một hình trụ với bán kính đáy 2m và chiều cao 5m, diện tích xung quanh sẽ là:
$$S_{xq} = 2 \times 3.14 \times 2 \times 5 = 62.8 \, m^2$$
3. Diện Tích Xung Quanh Hình Cầu
Hình cầu là một hình dạng có ứng dụng rộng rãi trong nhiều lĩnh vực. Công thức tính diện tích xung quanh của hình cầu là:
$$S_{xq} = 4\pi r^2$$
Trong đó:
- (r) là bán kính của hình cầu
Ví dụ, nếu bạn có một hình cầu với bán kính 3m, diện tích xung quanh sẽ là:
$$S_{xq} = 4 \times 3.14 \times 3^2 = 113.04 \, m^2$$

4. Diện Tích Xung Quanh Hình Nón
Hình nón là một hình dạng đa diện có một đỉnh và một đáy hình tròn. Công thức tính diện tích xung quanh của hình nón là:
$$S_{xq} = \pi rl$$
Trong đó:
- (r) là bán kính đáy của hình nón
- (l) là đường sinh của hình nón
Ví dụ, nếu bạn có một hình nón với bán kính đáy 2m và đường sinh 5m, diện tích xung quanh sẽ là:
$$S_{xq} = 3.14 \times 2 \times 5 = 31.4 \, m^2$$
5. Diện Tích Xung Quanh Hình Lăng Trụ
Hình lăng trụ là một hình dạng đa diện đặc biệt với hai đáy là hai hình đa diện giống nhau và các cạnh bên là các đoạn thẳng nối các đỉnh tương ứng của hai đáy. Công thức tính diện tích xung quanh của hình lăng trụ là:
$$S_{xq} = P \times h$$
Trong đó:
- (P) là chu vi đáy của hình lăng trụ
- (h) là chiều cao của hình lăng trụ
Ví dụ, nếu bạn có một hình lăng trụ với chu vi đáy 10m và chiều cao 6m, diện tích xung quanh sẽ là:
$$S_{xq} = 10 \times 6 = 60 \, m^2$$
Ứng Dụng Thực Tế và Tài Liệu Tham Khảo
Việc nắm vững các công thức tính diện tích xung quanh không chỉ giúp bạn giải quyết các bài toán trong học tập mà còn có thể áp dụng vào thực tế, như trong thiết kế kiến trúc, xây dựng, và các ngành kỹ thuật khác. Để có thêm thông tin chi tiết và các ví dụ minh họa, bạn có thể tham khảo trang web sdrc.com.vn, nơi cung cấp nhiều tài liệu hữu ích và các bài giảng trực tuyến về toán học và các môn khoa học khác.
Kết Luận
Việc hiểu và áp dụng các công thức tính diện tích xung quanh là rất quan trọng trong nhiều lĩnh vực. Hy vọng bài viết này đã cung cấp cho bạn những kiến thức cần thiết và hữu ích. Đừng quên truy cập sdrc.com.vn để cập nhật thêm nhiều thông tin và tài liệu học tập bổ ích.














